Relish the Moment
Learn Symbolic Execution and angr
TyeYeah Lv4
  2020-03-05 15:49:12   2020-11-12 21:23:54    2k Words  12 Mins

Besides Fuzzing, Symbolic Execution is another choice to approach reverse engineering and binary analysis.

Symbolic Execution Intro

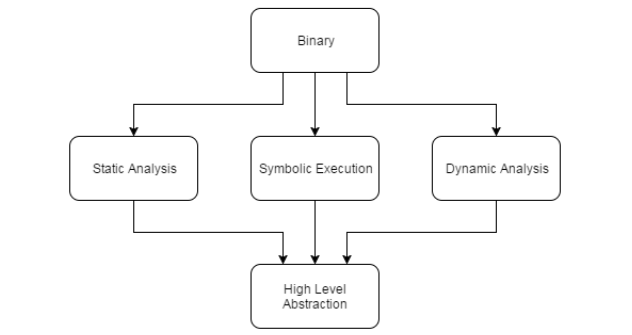
reverse engineering concept diagram

This is a general reverse engineering concept diagram.

The second layer shows that there are multiple reverse engineering methods that fall under different categories.

Symbolic execution is a method that falls between static analysis and dynamic analysis.

Basic principle

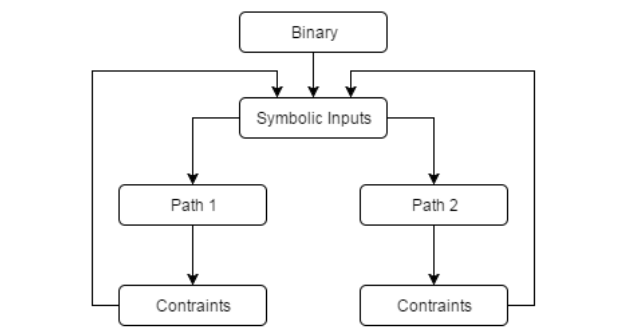
symbolic execution flow chart

This is a flow chart for general symbolic execution.

The execution starts by creating symbolic inputs from the original binary.

From the inputs, paths can be deduced and each path will carry certain constraints.

The inputs from these constraints will then be executed upon until all paths are found.

Example

eg

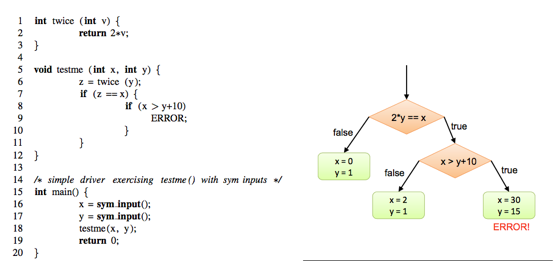
All execution paths of a program can be represented as a tree –> execution tree

To explore paths, formally, symbolic execution maintains two variables globally:

  • σ : maps variable to symbolic expression
  • PC: symbolic path constraints

When symbol execution starts, the σ is empty and the PC is true.

In main we meet a read statement whose form is var = sym_input(). After execution a var -> s is added to σ . We will get: σ={ x->x0, y->y0 }.

The assignment statement like var = expression is the same, so after line6, we get: σ={ x->x0, y->y0, z->2y0 }.

When we meet conditional statements if(e) S1 else S2, two updates for PC.
Update PC –> PC ∧ σ(e) to represent then branch.
Create PC' –> PC ∧ ¬ σ(e) to represent else branch.

After line 7, we get two symbolic execution instances and path constraints are: x0 = 2y0 and x0 ≠ 2y0
After line 8, Another two instances and PC: (x0 = 2y0) ∧ (x0 > y0 + 10) and (x0 = 2y0) ∧ (x0 ≤ y0 + 10)

If things satisfy neither of the conditions, or program breaks, instance terminates. We can use constraint solver to generate values which leads to specific path.

Example above belongs to classical symbolic execution, pure static symbolic execution. There are two tricky problems resulting in its impractical:

  • what if loop occurs?
  • what if constraint solver cannot solve?

Concolic Execution

Key element of modern symbolic execution technology is their ability to mix concrete execution with symbolic execution.

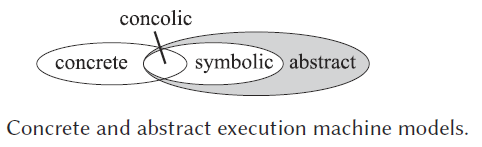
concolic

Concolic maintains two states:
Concrete State: maps all variables to their concrete values.
Symbolic State: only maps variables that have non-concrete values.

We use the previous example to see this process. Concolic execution first generates some random input: {x = A, y = B}(A ≠ 2B).

When it goes to the first fork, it adds x0 ≠ 2y0 to path constraints. Then reverse conjunction, to solve x0 = 2y0.

We can get {x = C, y = 2C}. When this input reaches next fork, then it does the same as above.

To sum up, it’s a process of testing inputs along with generating new inputs using constraint solver. Finally we explore all feasible paths.

Concolic execution deals problems of classic static symbolic execution – just replace tricky parts for solver with actual values. Meanwhile you’ll sacrifice the completeness of path exploration.

Challenges

Next let’s talk about challenges and solutions.

Path Explosion

Symbolic execution implicitly filtering two paths:

  • Paths not depending on symbolic input
  • Paths without solutions for current path constraint.

Though it is, path explosion is still the biggest chanllenge. There’re also two solutions:

  • Heuristics for path-finding (heuristic search) to increase code coverage
    • Interleave random testing (choose randomly)
    • Guided by CFG (control flow graph)
    • Combine with evolutionary search (fitness functionfor driving the exploration of the input space)
  • Reduce execution time by parallelizing independent pathsor by merging similar paths
    • Merge paths statically, then feed solver
    • Record and reuse results of low-level functions
    • Pruning redundant paths

Constraint Solving

It is a bottleneck in symbolic execution. The optimization of the solver (improving solving ability) has become a method to solve it.

Two solutions for it:

  • Irrelevant constraint elimination
  • Incremental solution: Caching constraints that have been solved to reuse

Memory Modeling

Precision of translation from statements to constraints, has a significant impact on the coverage obtained by symbolic execution.

When accessing memory and referencing a memory unit, whose reference comes from user input, the memory address becomes an expression.

Sometimes it’s a question about when to set this reference a concrete value, or whether use values to approximate some variables.

Precision or scalability, it’s a trade-off.

You have to consider:

  • Whether application code from high level, or system code from low-level
  • Practical effects of different constraint solvers

Handling Concurrency

Large programs are usually concurrent. Because of the inherent nature of such programs, dynamic symbolic execution systems can be used to efficiently test concurrent programs, including applications for complex data entry, distributed systems, and GPGPU programs.

angr Intro

angr is a binary analysis framework developed by researchers from the Computer Security Lab at UC Santa Barbara.

The tool provides binary analysis information such as finding functions and generating function call graphs and it also includes a symbolic solver engine capable of performing symbolic execution.

angr can be a significant part of expanding the field of reverse engineering not only because of its symbolic execution engine, but also because of its strengths as a binary analysis tool. Its ability to find functions and generate function call graphs are important to reverse engineering.

Documentation as HTML and as a Github repository. They are very helpful.

Installation

It is documented in docs.angr.io/introductory-errata/install.

Though use pip install angr is pretty easy, I still recommend to get it by virtualenv or docker, which is recommended by official. There are old version lib dependencies that will mess your environment up.

Despite running script, using IPython to run command is also encouraged.

Symbolic Execution Example

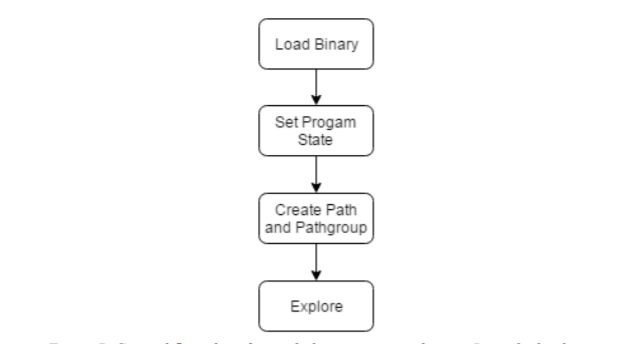
flow chart

This is a general flow chart for symbolic execution with angr. Begin by loading the binary with parameters, set the program state to begin at, then create the path and pathgroup to explore on.

Simple Solution 0x00

Here we write demo check.c ourselves. It contains a simple fork when guessing the string.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<stdio.h>
void success(){
    printf("success\n");
    printf("here is your flag if it's a ctf\n");
}
void failed(){
    printf("failed\n");
}
int main(void){
    char check[9];
    scanf("%s",check);
    if(!strcmp(check,"p4ssw0rd")){
        success();
    }else{
        failed();
    }
    return 0;
}

Main logic is to input specific word to activate success method.
Now we use angr to analyse it.

You should have read docs.angr.io/core-concepts and known basic properties.
Then we follow the flow chart to do.

First we load the library

1
2
import angr
p = angr.Project("./check",auto_load_libs=False) # normally False

If you need logging, add this

1
2
import logging
logging.getLogger('angr.manager').setLevel(logging.DEBUG)

Then set the program state to start

1
2
state=p.factory.entry_state()           # if Project is an "initialization image", here is 'simulated program state'
sm=p.factory.simulation_manager(state)  # simulation_manager is like a simulator

After that we begin to explore

1
2
3
4
5
6
7
res = sm.explore(find=lambda s: b"flag" in s.posix.dumps(1))    # explore to find path where b'flag' appears
print (len(res.found))                                          # see if there's a result
if len(res.found) > 0:
    print('Your input should be: ',res.found[0].posix.dumps(0))
    print('And result looks like: ',res.found[0].posix.dumps(1))
# the output may be messed by random bytes, because it's a memory dump
# but key info exists, and in this way we find a flag

Here is the final script

1
2
3
4
5
6
7
8
9
10
11
12
from angr import *
import logging
logging.getLogger('angr.manager').setLevel(logging.DEBUG) 
p = Project("./check",auto_load_libs=False)
state=p.factory.entry_state()
sm=p.factory.simulation_manager(state)
res = sm.explore(find=lambda s: b"flag" in s.posix.dumps(1))        # change b"flag" to bytes you want 
print (len(res.found))                                              # angr has an engine to help you
if len(res.found) > 0:
    print('Your input should be: ',res.found[0].posix.dumps(0)) 
    print('And result looks like: ',res.found[0].posix.dumps(1))

Output is like

1
2
3
1
Your input should be:  b'p4ssw0rd\x00J\x00\x08\x00\x02\x02\x08I\x02)\x00\x89\x06I\x02\x00\x01\x02\x01\x08\x01\x02\x00\x01\x00\x01\x00\x01\x02\x00\x08\x00\x01\x00\x02\x00\x00\x00\x00\x00\x02\x00\x02\x04\x89\x89\x00\x00\x00\x00\x00'
And result looks like:  b"success\nhere is your flag if it's a ctf\n"

Simulation Execution 0x01

We have the same check to analyse, with different script

1
2
3
4
5
6
7
8
9
10
11
12
13
import angr
proj = angr.Project('./check')
state = proj.factory.entry_state() 
forknum = 2                                     # normally is path number when encounter a fork
while True:
    succ = state.step()                         # 'state' is used like a simulator. kind of like 'unicorn'
    if len(succ.successors) == forknum:         # if we meet a fork, having specific number paths to go
        break
    state = succ.successors[0]                  # we break the point and check state

state1, state2 = succ.successors
print('Fork 1 dump is:',state1.posix.dumps(0))
print('Fork 2 dump is:',state2.posix.dumps(0))

Then we can have

1
2
Fork 1 dump is: b'p4ssw0rd\x00\x00\x02\x00\x02\x00\x00\x00\x00\x02\x02\x02I\x00\x02\x00\x00\x01\x02\x02\x01\x01\x02\x08\x00\x08\x00\x01\x00\x00\x00\x01\x00\x00\x19\x01\xa0\x00\x00\x00\x08\x00\x00\x00\x00\x00\x80\x08\x00\x00\x00\x01'
Fork 2 dump is: b'\x01\x0e\x00\x00\x89\x00\x04"IJ\x00\x08\x89\x00\x19\xa4I\x0e\x8a\x01\x03\x02I*J\x00\x89II\x02\x00@\x8a@\x02\x89\x89\x02\x02I\x00\x01\x08\x89\x82\x89\x00\x0f\xd9*\x19\x89\x02\x02\x01@\x02\x02\x02\x00'

Pass Arguments 0x02

We write another demo check2.c to learn about passing args.
And we compile without PIE to try another way of exploring.

1
2
3
4
5
6
7
8
9
10
11
12
#include <stdio.h>
#include <string.h>
int main(int argc, char** argv)
{
    if (!strcmp(argv[1], "hello args test")) {
        printf("you win!");
    }
    else {
        printf("you lose!");
    }
    return 0;
}

Solver engine of angr is called Claripy.
The way we pass command line arguments is 

1
2
3
4
5
args = claripy.BVS("args", 8 * 16)                      
# create a bitvector symbol named "args" of length 8 * 16 bits
# state.solver.BVV(num, size) is used to set value with exact number and size
state = p.factory.entry_state(args=['./check2', args])  
# in this way we pass args

Because we remove PIE, no randomization for address.
Use objdump to disassemble

1
2
3
4
5
6
7
8
9
$ objdump -D check2

...
  401153:       48 89 c7                mov    %rax,%rdi
  401156:       e8 e5 fe ff ff          callq  401040 <strcmp@plt>     # Here is 'strcmp' call
  40115b:       85 c0                   test   %eax,%eax
  40115d:       75 13                   jne    401172 <main+0x40>      # a jump for not equal
  40115f:       48 8d 3d a7 0e 00 00    lea    0xea7(%rip),%rdi        # i guess it'sfor equal
...

So we can use absolute address to explore

1
2
3
sm = p.factory.simgr(state)             # another way for simulation
sm.explore(find=0x40115f)               # use address(when no PIE)
st = sm.found[0]                        # store the result(state)

And final script is

1
2
3
4
5
6
7
8
9
import angr
import claripy
p = angr.Project("./check2")
args = claripy.BVS("args", 8 * 16)
state = p.factory.entry_state(args=['./check2', args])
sm = p.factory.simgr(state)
sm.explore(find=0x40115f)
st = sm.found[0]
print st.se.eval(args,cast_to=str)      # solve the constraint

Output is 

1
g3t fl4g���

Then we guess the key word is “g3t fl4g”

Summary

angr is not only a gadget for symbolic execution but a tool for reverse engineering.
What I show you here is simple implementation for simple puzzles related with symbolic execution.
See angr examples to learn advanced techniques of angr.

  1. 1. Symbolic Execution Intro
    1. 1.1. Basic principle
    2. 1.2. Example
    3. 1.3. Concolic Execution
    4. 1.4. Challenges
      1. 1.4.1. Path Explosion
      2. 1.4.2. Constraint Solving
      3. 1.4.3. Memory Modeling
      4. 1.4.4. Handling Concurrency
  2. 2. angr Intro
    1. 2.1. Installation
    2. 2.2. Symbolic Execution Example
      1. 2.2.1. Simple Solution 0x00
      2. 2.2.2. Simulation Execution 0x01
      3. 2.2.3. Pass Arguments 0x02
    3. 2.3. Summary
© 2018 - 2024    TyeYeah
Powered by Hexo & Theme Keep
Total words 135.7k
  1. 1. Symbolic Execution Intro
    1. 1.1. Basic principle
    2. 1.2. Example
    3. 1.3. Concolic Execution
    4. 1.4. Challenges
      1. 1.4.1. Path Explosion
      2. 1.4.2. Constraint Solving
      3. 1.4.3. Memory Modeling
      4. 1.4.4. Handling Concurrency
  2. 2. angr Intro
    1. 2.1. Installation
    2. 2.2. Symbolic Execution Example
      1. 2.2.1. Simple Solution 0x00
      2. 2.2.2. Simulation Execution 0x01
      3. 2.2.3. Pass Arguments 0x02
    3. 2.3. Summary